hash_ops.c File Reference
Hash operations for copy/move detection. More...
#include <fcntl.h>#include "global.h"#include "waa.h"#include "helper.h"#include "hash_ops.h"
Go to the source code of this file.
Data Structures | |
| struct | hsh___list |
| Structure for storing a number of data packets of size sizeof(void*). More... | |
Functions | |
Simple hash functions. | |
| int | hsh___new_bare (char *wcfile, char *name, int gdbm_mode, GDBM_FILE *output, char **fname_out) |
| Bare open function for internal use. | |
| int | hsh__new (char *wcfile, char *name, int gdbm_mode, hash_t *output) |
| -. | |
| int | hsh__collect_garbage (hash_t db, int *did_remove) |
| -. | |
| int | hsh__close (hash_t db, int has_failed) |
| -. | |
| int | hsh__fetch (hash_t db, datum key, datum *value) |
| -. | |
| int | hsh__first (hash_t db, datum *key) |
| -. | |
| int | hsh__next (hash_t db, datum *key, const datum *oldkey) |
| -. | |
| int | hsh__store (hash_t db, datum key, datum value) |
| -. | |
| int | hsh__store_charp (hash_t db, char *keyp, char *valuep) |
| -. | |
Hash list manipulation. | |
| int | hsh__insert_pointer (hash_t hash, datum key, void *value) |
| -. | |
| int | hsh__list_get (hash_t hash, datum current_key, datum *next_key, struct estat **arr[], int *found) |
| -. | |
| int | hsh__register_delete (hash_t db, datum key) |
| Registers some key for deletion on database close. | |
Detailed Description
Hash operations for copy/move detection.
The hash operations are binary clean; they don't care what kind of key/value data they store.
Storage considerations
The basic question is ... do we need an unlimited amount of list entries in any hash bucket, or do we not?
If we do, we have these possibilities:
Extending the key, counting entries.
The first entry is written as now.
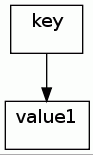
If we find a second entry with the same key,
- it is written as
{key}1 - and the other one as
{key}2; - the
{key}entry is set to the integer2, (which can easily be distinguished because of the length)Every further entry with the same key would increment the counter, and get stored at that position.
That's not optimal for performance: - It means reading a value (does the key exist?), and
- possibly writing that key with another value again, and
- storing a value. Note that this would require some end-of-key marker (like
\0), or keys with a constant length.
Storing a linked list in the hash.
Every entry is written with a header; the first for some given key gets the number 0, as an end-of-list marker.

If this key has a collision, we
- increment the stored
number, - write the old value under the key
{number}, with the header set to 0. - The new value gets the current
numberprepended, and stored with the givenkey.After several insertions, the situation might be like this: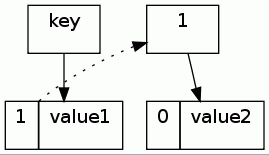
Storing a verbatim array
If there's a limited number of entries (with known length) to store, an array with a defined size might be easiest.
A similar variant would be to simply concatenate the data in the hash buckets, with some suitable separator.
- memory intensive, slow for big buckets (many bytes to copy).
- For array iteration some special convention for the
keywould have to be used, like.dsize=0 and.dptr=array_def; the last returned index would have to be stored in the array structure. - Big advantage: fast for reading, doesn't have to seek around.
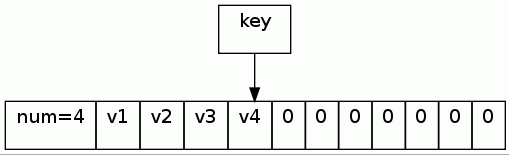
Conclusio
Barring other (better) ideas, the array solution is currently implemented; the array is of fixed-size, can store only pointers, and the function for getting a list allows returning a set of elements.
Definition in file hash_ops.c.
Function Documentation
| int hsh___new_bare | ( | char * | wcfile, | |
| char * | name, | |||
| int | gdbm_mode, | |||
| GDBM_FILE * | output, | |||
| char ** | fname_out | |||
| ) |
Bare open function for internal use.
*fname_out, if not NULL, gets an allocated copy of the filename.
STOPIF_CODE_ERR
- Todo:
- remove this bugfix sometime ...
Definition at line 184 of file hash_ops.c.
References GWD_MKDIR, HASH_TEMPORARY, hlp__strdup(), STOPIF, STOPIF_CODE_ERR, waa__get_gwd_flag(), waa__get_waa_directory(), waa_tmp_fn, and waa_tmp_path.
Referenced by hsh__new(), and hsh__register_delete().


| int hsh__close | ( | hash_t | db, | |
| int | has_failed | |||
| ) |
-.
Close a property file.
If has_failed is set, some error has happened, and the registered keys are not used for deletion (like a ROLLBACK).
Definition at line 326 of file hash_ops.c.
References hash_s::db, DEBUGP, hash_s::filename, hsh__collect_garbage(), hsh__first(), IF_FREE, STOPIF, hash_s::to_delete, and waa__delete_byext().
Referenced by ci___send_user_props(), cm___dump_list(), cm___get_base_source(), cm___make_copy(), cm__detect(), prp__g_work(), prp__l_work(), prp__open_get_close(), prp__s_work(), prp__set_from_aprhash(), and up__fetch_decoder().


| int hsh__collect_garbage | ( | hash_t | db, | |
| int * | did_remove | |||
| ) |
-.
Collect garbage in the hash table.
The previously marked keys in the hash table are removed; it is not checked for empty-ness nor reorganized.
Definition at line 287 of file hash_ops.c.
References hash_s::db, DEBUGP, STOPIF_CODE_ERR, and hash_s::to_delete.
Referenced by hsh__close().
| int hsh__fetch | ( | hash_t | db, | |
| datum | key, | |||
| datum * | value | |||
| ) |
-.
Read value associated with some key in db.
Definition at line 378 of file hash_ops.c.
References hash_s::db, and IF_FREE.
Referenced by cm___dump_list(), cm___get_base_source(), hsh__insert_pointer(), hsh__list_get(), and prp__fetch().

| int hsh__first | ( | hash_t | db, | |
| datum * | key | |||
| ) |
-.
Find first key.
Definition at line 394 of file hash_ops.c.
References hash_s::db.
Referenced by cm___dump_list(), hsh__close(), and prp__first().
| int hsh__insert_pointer | ( | hash_t | hash, | |
| datum | key, | |||
| void * | value | |||
| ) |
-.
For short-time storage (single program run): Insert the pointer value into the hash at key.
Definition at line 494 of file hash_ops.c.
References BUG_ON, hsh___list::count, hsh___list::entries, HASH__LIST_MAX, hsh__fetch(), hsh__store(), and STOPIF.
Referenced by cm___hash_register().

| int hsh__list_get | ( | hash_t | hash, | |
| datum | current_key, | |||
| datum * | next_key, | |||
| struct estat ** | arr[], | |||
| int * | found | |||
| ) |
-.
Get an list of found entries from hash addressed by current_key into the (statically allocated) arr.
If next_key is not NULL, it is set so that the next query can use this key for the next element. If *next_key==NULL, no next element is there; everything has been returned. If no (more) entry could be found, ENOENT is returned, and *found==0.
In case of storage via an array hsh__list must store some internal state; therefore only a single loop is (currently) possible.
Definition at line 563 of file hash_ops.c.
References BUG_ON, hsh___list::count, hsh___list::entries, HASH__LIST_MAX, hsh__fetch(), and STOPIF.
Referenced by cm___hash_list(), and cm___match_children().

| int hsh__new | ( | char * | wcfile, | |
| char * | name, | |||
| int | gdbm_mode, | |||
| hash_t * | output | |||
| ) |
-.
Create a new hash for wcfile with the given name.
If flags is GDBM_NEWDB, the file gets deleted immediately; there's no need to keep it around any longer, and it's not defined where it gets located. If another open mode is used, the entry is always created in the WAA or CONF base directory for wcfile, ie. the hashed path for the working copy root.
Definition at line 258 of file hash_ops.c.
References hash_s::db, hash_s::filename, HASH_REMEMBER_FILENAME, hlp__calloc(), hsh___new_bare(), IF_FREE, and STOPIF.
Referenced by cm___dump_list(), cm___get_base_source(), cm___make_copy(), cm__detect(), and prp__open_byname().

| int hsh__next | ( | hash_t | db, | |
| datum * | key, | |||
| const datum * | oldkey | |||
| ) |
-.
Find next key.
If oldkey==key the ->dptr is free()d; else the caller has to do that.
Definition at line 410 of file hash_ops.c.
References hash_s::db, and IF_FREE.
Referenced by cm___dump_list(), and prp__next().
| int hsh__register_delete | ( | hash_t | db, | |
| datum | key | |||
| ) |
Registers some key for deletion on database close.
Definition at line 609 of file hash_ops.c.
References DEBUGP, HASH_TEMPORARY, hsh___new_bare(), STOPIF, STOPIF_CODE_ERR, and hash_s::to_delete.
Referenced by ci___send_user_props(), and cm___get_base_source().


| int hsh__store | ( | hash_t | db, | |
| datum | key, | |||
| datum | value | |||
| ) |
-.
Store some value in the hash table.
Definition at line 432 of file hash_ops.c.
References hash_s::db, and STOPIF_CODE_ERR.
Referenced by hsh__insert_pointer(), hsh__store_charp(), and prp__store().

| int hsh__store_charp | ( | hash_t | db, | |
| char * | keyp, | |||
| char * | valuep | |||
| ) |
-.
Store character strings in the hash table.
The delimiting \0 is stored, too.
Definition at line 451 of file hash_ops.c.
References hsh__store().
Referenced by cm___make_copy().

 1.6.1
1.6.1